Zur Themenübersicht     

Eigenschaften von AVL-Bäumen

Bei den AVL-Bäumen (nach Adelson, Velskii und Landis benannt) handelt es sich um beinahe ausgeglichene Binärbäume. 

Definition: Dabei gilt für jeden Knoten des AVL-Baumes die Bedingung, dass sich die Höhe der beiden untergeordneten Teilbäume höchstens um 1 unterscheiden darf. 

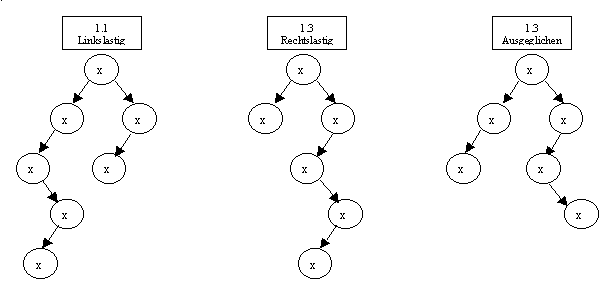
Diese Lösung stellt einen guten Kompromiss zwischen einer geringen Gesamthöhe des Baumes und einem relativ geringen Aufwand beim Einfügen, sowie Löschen von Elementen dar. In der Praxis wird für jeden Knoten der Grad der Ausgeglichenheit gespeichert, wobei zwischen linkslastig, völlig ausgeglichen und rechtslastig unterschieden wird (siehe Beispielzeichungen 1.1, 1.2, 1.3). Die geringe Gesamthöhe ist insofern wünschenswert, da sich die Laufzeit zum Suchen proportional zur Höhe des Baumes verhält. Wenn man die AVL-Bäume mit den "normalen" Binärbäumen vergleicht, so kann man erkennen, dass aufgrund des hohen Aufwandes beim Löschen und Einfügen, der bei den "normalen" Binärbäumen nötig ist, die AVL-Bäume insbesondere für Bereiche geeignet sind, in denen auf einen fest vorgegebenen Datenbestand viel Zugriffe erforderlich sind, insbesondere wenn auf alle Knoten im Mittel gleich oft zugegriffen wird. 

Rotieren

Es gibt verschiedene Wege einen ausgeglichenen Baum zu implementieren. Es gibt zum einen die oben erwähnten AVL-Bäume oder die Rot-Schwarz-Bäume, auf die ich aber nicht näher eingehen möchte. Diese Bäume überwachen den Baum hinsichtlich seines Grades der Ausgeglichenheit. Um einen Baum aber auszugleichen, benutzen sie alle die gleiche Methode, das Rotieren.

Beim Rotieren werden die Knoten im Baum neu angeordnet. Dies geschieht dadurch, dass bestimmte Knoten näher zur Wurzel gebracht werden, und andere sich von der Wurzel entfernen. Gleichzeitig wird darauf geachtet, dass die Regeln eines binären Suchbaumes nicht verletzt werden. Der Ausdruck Rotieren kann allerdings etwas missverstanden werden. Nicht die Knoten werden rotiert, sondern die Beziehungen zwischen ihnen. Dies geschieht durch das Umbiegen von Zeigern. Bei einer Rotation wird nie nur ein Knoten rotiert, sondern es gibt einen "top"-Knoten, um den herum rotiert wird. Es gibt zwei verschiedene Arten der Rotation, die Rechts-Rotation und die Links-Rotation.

Rechtsrotation um die Wurzel (70) bei folgendem Baum:

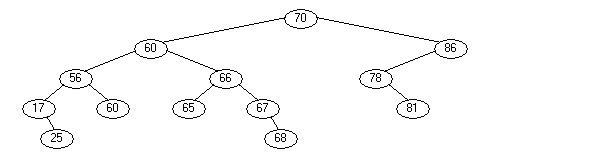
Ich werde nun eine einfache Rechtsrotation durchführen. 

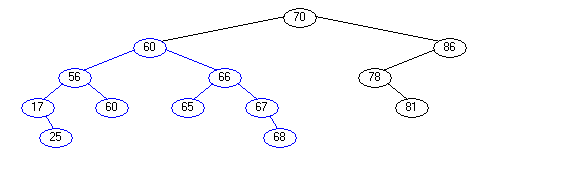
Dabei ist hier der "top"-Knoten der Knoten mit dem Inhalt 70. Der linke Teilbaum (oben blau markiert) wird der Ersetzer-Baum und seine Wurzel mit dem Inhalt 60 wird der "Ersetzer"-Knoten für den "top"-Knoten. 

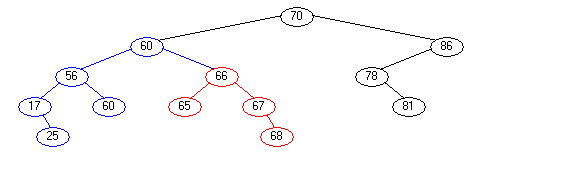
Hierfür wird in einem ersten Schritt der gesamte rechte Teilbaum des "Ersetzer-Baumes" (oben rot) links an den Top-Baum angehängt. 

Warum wird hier die Ordnung des Baumes beibehalten? Der rote Teilbaum stammt ja aus dem linken Teilbaum des Topbaumes. Also sind alle Knoteninhalte kleiner als der Top-Knoten. Also dürfen wir den roten Teilbaum links an den Top-Knoten anhängen.

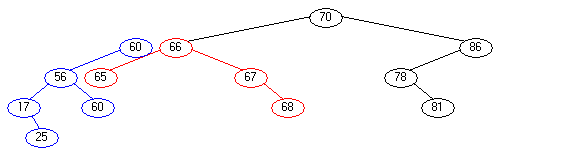
In dieser Grafik wird deutlich, dass der Ersetzer-Baum dafür von der Wurzel des Top-Baumes getrennt wird. Es existieren in diesem Moment also zwei Bäume, die seperat verwaltet werden. Ferner hat der Ersetzer-Baum keinen rechten Teilbaum mehr. (Der wurde ja umgehängt). An diese freie Stelle hängen wir nun den Top-Baum an. 

Warum bleibt auch hierbei der Baum geordnet? 
Die Knoten des rechten Zweiges  des ursprünglichen Top-Baumes (beginnend mit 86), sind eh größer als die Wurzel des Ersetzer Baumes (60), die ja aus dem linken Teilbaum stammt. 
Dei Inhalte des nun neuen linken Teilbaumes des Top-Baumes (oben rot) stammen aus dem rechten Teilbaum des Ersetzer Baumes, sind also auch alle größer als dessen Wurzel (6). 

Also: Die Operation liefert wieder einen geordneten Suchbaum, nämlich:

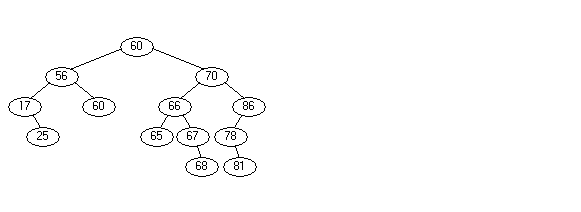
Eigentlich ist die Operation damit beendet. Führen wir sie aber in der Mitte eines Baumes durch, müssen wir noch diesen jetzt entstandenen Baum wieder zum Top-Baum machen. Daher zeigt die folgende Grafik den Baum am Ende der Rotation:

Danach hat sich der Baum wesentlich verändert. Der Beispiel-Baum ist in diesem Stadium übrigens nicht ausgeglichen!! Hier sollte nur der Vorgang der Rotation dargestellt werden! Wie ein Baum sinnvoll ausgeglichen werden kann, zeigt erst die nächste Seite.

Zur Themenübersicht
Zum Seitenanfang
Zur vorigen Seite	Zur nächsten Seite