Zur Themenübersicht     

Definition

Ein EEA oder kurz EA unterscheidet sich von einem gewöhnlichen endlichen Automaten darin, dass er 

1. keine Ausgabefunktion besitzt und 
2. die Menge der Zustände in akzeptierte- und nicht akzeptierte Zustände zerfällt:

    Menge der Zustände      Z    =  Z_a  È  Z_f             

            Z_a   akzeptierende Zustände  
            Z_f   nicht akzeptierende bzw. Fehlerzustände

Erkennende Automaten werden hauptsächlich zur Analyse von Eingabemengen bzw. Eingabefolgen genutzt.

1.1 Beispiel

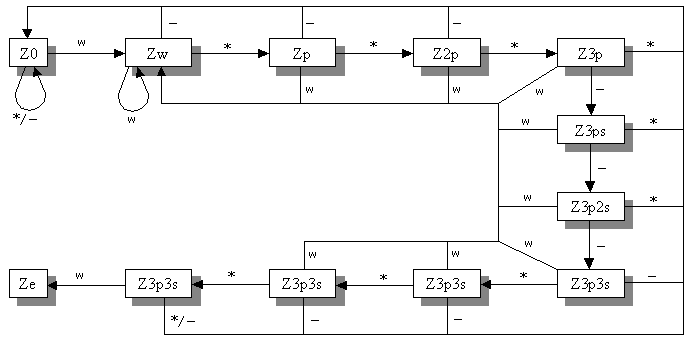
Ein "SOS" erkennender Automat ):

Dieser Automat soll erkennen, ob die Zeichenfolge SOS, In der Morseform: w * * * - - - * * * w , vorliegt.
Dabei bedeuten  ' * ' = Punkt , ' - ' = Strich , ' w ' = warten 

E = { ' * ' , ' - ' , ' w ' }                                                                 

Z = { Z0,Zp,Z2p,Z3p,Z3ps, Z3p2s, Z3p3s, Z3p3sp, Z3p3s2p, Z3p3s3p,Ze }

Z _a = { Ze }        

Z _f  = { Z0,Zp,Z2p,Z3p,Z3ps, Z3p2s, Z3p3s, Z3p3sp, Z3p3s2p, Z3p3s3p}       

1.2 Graphische Darstellung der Übergangsfunktion dieses Automaten:

1.3 Eine Mögliche Realisierung in Delphi

Durch die Verschachtlung der 

'case' - Anweiungen kommt die 

Übergangsfunktion zustande.

In der Übergeordneten 'case'-abfrage

wird der aktuelle Zustand z  

berücksichtigt, während die untergeordneten

Abfragen durch den aktuellen character e 

dann den jeweiligen neuen Zustand

 bestimmen.

Function TForm1.f (z :TZustand ; e :char): TZustand;
begin

 case z of

	Z0:   case e of

		     'w' result := Zw;

                   else	 result := Z0;

	Zw:   case e of

		...

	end; { of case of z}
end;

Zur Themenübersicht
Zum Seitenanfang
Zur vorigen Seite	Zur nächsten Seite