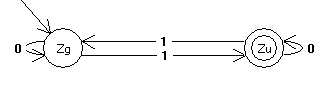Zur Themenübersicht     

Aufgaben zu EA's 1

Aufgaben:

  1. In den Vereinigten Staaten wünscht die League Against Sexist Speech ein Programm, das in allen Texten die Zeichenfolge „man“ finden und durch „person“ ersetzen kann. Z. B. soll aus dem „travelling salesman“ eine „travelling salesperson“ gemacht werden.
    Entwerfe einen Automaten, der in einem vorgegebenen Text erkennt, ob dieser auf  „man“ endet.
  2. Paritätsprüfung (Paritätsbits werden oft als einfaches Mittel zur Fehlererkennung eingesetzt):
    Gib einen Automaten an, der prüft, ob eine Dualzahl eine ungerade Anzahl von Einsen enthält.
  3. Gesucht ist ein Automat, der untersucht, ob eine Dualzahl durch die Zahl 4 teilbar ist. Anders formuliert:
    gesucht ist ein Automat, der erkennt, ob eine Dualzahl auf 100 endet.
  4. Ein Spieler spielt gegen die Bank. Er wirft wiederholt einen Würfel. Er hat das Spiel verloren, sobald er eine gerade Zahl gewürfelt hat, er hat gewonnen, sobald eine 1 und eine 3 (in beliebiger Reihenfolge) gefallen sind.
    Wenn eine 5 gewürfelt wird, darf er weiterwürfeln.
    Beispiele für Gewinnfolgen sind: 1,5,3 oder 5,5,3,3,1
    Beispiele für Verlustfolgen sind: 1,5,2 oder 4 oder auch 3,5,6
    Setze die Spielregeln in einen endlichen Automaten um.

Lösungen:

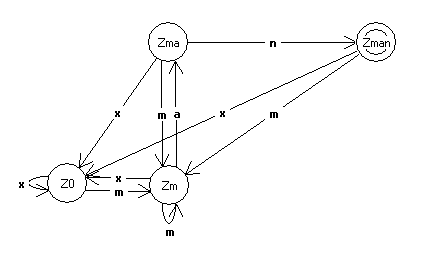
zu 1) Bei diesem Automaten gibt es 4 verschiedene Zustände.


Eingaben  gibt es ebenfalls 4, also E = {m,a,n,x}, dabei steht x immer für alle Buchstaben, für die kein Folgezustand angegeben ist.


zu 2) Bei diesem Automaten gibt es 2 verschiedene Zustände.
  • Zg: Dies ist der Ausgangszustand. Kommt nun eine "1" vor, wird in den Zustand "Zu" gewechselt. Bei einer "0" bleibt er in diesem Zustand.
  • Zu: Dies ist der Zustand, wenn bisher eine ungerade Anzahl "1en" vorkamen. Kommt nun wieder eine "1" vor, dann geht es zurück in den Zustand "Zg". Bei einer "0" bleibt er in diesem Zustand! 
    Da auf eine ungerade Anzahl von Einsen geprüft werden soll, ist dies der akzeptierende Zustand.
    •

    Das Eingabealphabet ist E = {0,1}

    Das Zustandsdiagramm ist sehr einfach:


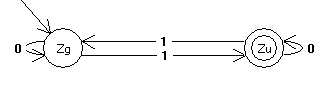
    zu 3) Das überlassen wir einmal dem geneigten Leser selbst !!

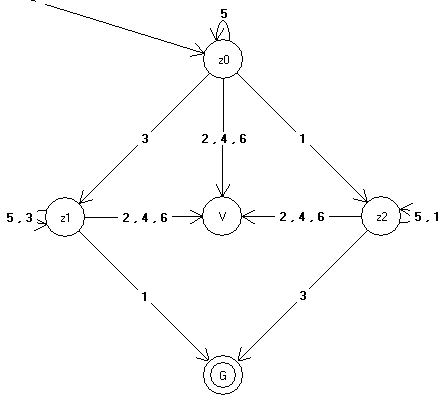
    zu 4) Bei diesem Automaten gibt es 5 verschiedene Zustände.

    Z0: Dies ist der Ausgangszustand. Bei den Ereignis 2,4 und 6 geht der Automat aus diesem Zustand in den Zustand "V". Bei einer "1" geht er in eben diesen Zustand, bei einer "5" ebenfalls in den gleichnamigen Zustand!
    Z1: Dies ist der Zustand, wenn bereits eine "3" gewürfelt wurde. Folgt nun ein 5 oder eine 3, bleibt er in diesem Zustand. Bei einer gewürfelten 1 wird in den Zustand "G" gewechselt. Bei den Ereignis 2,4 und 6 geht der Automat aus diesem Zustand in den Zustand "V".
    Z2: Dies ist der Zustand, wenn bereits eine "1" gewürfelt wurde. Folgt nun ein 5 oder eine 1, bleibt er in diesem Zustand. Bei einer gewürfelten 3 wird in den Zustand "G" gewechselt. Bei den Ereignis 2,4 und 6 geht der Automat aus diesem Zustand in den Zustand "V".  - V: (Verloren) Dies ist der Zustand, wenn eine gerade Zahl, d.h. 2,4 oder 6 gewürfelt wurde. Aus diesem Zustand kann man nicht mehr raus, egal was gewürfelt wird.
    G: (Gewonnen, akzeptierter Zustand) Der Finalzustand: In diesem Zustand sind bereits eine 1 und eine 3 gefallen. Der Spieler hat gewonnen!

    Eingabealphabet : E = {1,2,3,4,5,6}

    Und schliesslich der Automat:




    Zur Themenübersicht  
    Zum Seitenanfang 
    Zur vorigen Seite         Zur nächsten Seite  

        © 2004 LK 13 If und G. Kubitz  Hannah-Arendt-Gymnasium, Lengerich