Informatik LK  13 , Abi  2002 (kub)

  Zur Themenübersicht     

AUTOMATENTHEORIE erstes Beispiel

Wir wollen uns einen Automaten am Beispiel eines Getränkeautomaten klarmachen:

Getränke: Fanta, Sprite, Wasser

Knöpfe: Es muss für jedes Getränk ein Knopf existieren:

Geldannahme: Der Einfachheit halber werden nur zwei Eingaben für das Geld erlaubt:

Mögliche Ausgaben: - 1 Flasche Fanta: AF (Ausgabe Fanta)

Vereinbarungen: 

1. Der Automat wechselt nicht, d.h.:

2. Nach Drücken der ER-Taste wir alles eingeworfene Geld wieder ausgeworfen.

3. Beim Drücken der Getränketaste und einem Guthaben von weniger als 1,5 DM passiert nichts.

 

Wir analysieren unseren Automaten etwas genauer, um allgemeine Aussagen über Automaten zu finden:

Die Knöpfe für die Getränke und die Geldannahme bilden bei diesem Automaten das Eingabealphabet, welches wie folgt aussieht:  Eingabealphabet:  E = {EF;ES;EW;E0,5;E1}.
Die möglichen Ausgaben des Automaten werden als Ausgabealphabet bezeichnet: Ausgabealphabet: A = {AF;AS;AW;A0,5;A1;A1,5}.
Der Automat kann verschiedene innere Zustände haben, die man in einer Zustandsmenge zusammenfasst:

Die Zustände geben in diesem Beispiel an, wie viel DM schon im Getränkeautomaten gespeichert sind. daher können sie auch für die Anzeige im Display des Automaten benutzt werden.

 Zustände:  Z = {C0;C0,5;C1;C1,5} 

(*C steht für Condition*)
Unser Automat hat (hoffentlich) keine Endzustände. (Ein Endzustand ist ein Zustand, der bei keiner Eingabe mehr geändert wird) Endzustände: M = { } 

Wir verallgemeinern unsere Überlegungen und geben eine allgemeine Definition eines endlichen Automaten (EA) an:

Definition eines endlichen Automaten:
  1. Ein endlicher Automat besitzt ein endliches Eingabealphabet E = {ei; e2; … en}
  2. Ein endlicher Automat besitzt ein endliches Ausgabealphabet A = {ai; a2; … an}
  3. Ein endlicher Automat besitzt eine endliche Zustandsmenge Z = {zi; z2; … zn}
  4. Bei einem endlichen Automaten existiert immer ein definierter Anfangszustand z0 Î Z
  5. Es gibt Menge möglicher Endzustände M Î Z 
  6. Die Übergänge von einem Zustand zu einem anderen Zustand werden durch eine  Übergangsfunktion f beschrieben: 

    f: ( zi Î Z ; ej Î E ) à z k Î Z

    Sie ordnet jedem Zustand und jeder möglichen Eingabe genau einen Folgezustand zu.
  7. Es existiert eine Ausgabefunktion 

    g: (zj Î Z ; ei Î E ) à ak Î A

    Sie ordnet jedem Zustand und jeder möglichen Eingabe eine Ausgabe zu.

Anmerkung: In diesem Fall sprechen wir von einem deterministischen endlichen Automaten, DEA.
Wenn es zu einem Zustand und einer Eingabe mehr als einen möglichen Folgezustand gibt, sprechen wir nicht von einem deterministischen sondern von einem nichtdeterministischen Automat: NEA.
Dann existiert keine Übergangsfunktion sondern eine Übergangsrelation.  

 

Um Übergangs- und Ausgabefunktion eines endlichen Automaten genauer zu beschreiben, kann man entweder ein Zustandsdiagramm (siehe Graphik hierunter) oder eine Zustandtabelle (siehe unten) erstellen.

Zustandsdiagramm:

Die möglichen Zustände werden durch Kreise dargestellt. Die Übergänge von einem Zustand zu einem anderen werden durch Pfeile verdeutlicht. An den Pfeilen stehen Eingabe und Ausgabe, getrennt durch einen senkrechten Strich. Mehrere mögliche Ein- und Ausgabepaare stehen untereinander.

 

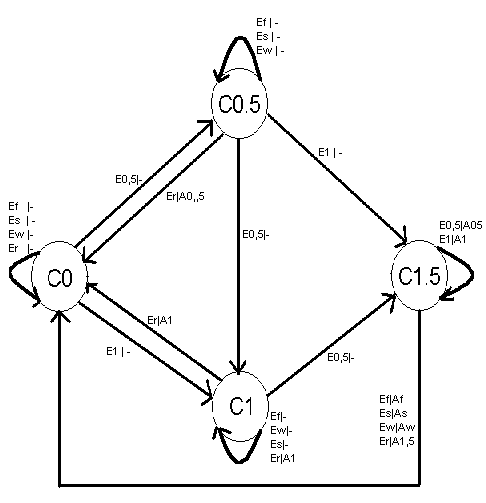
Zustandstabelle: 

Zustandstabellen geben die selbe Information in anderer Form aus. Hier sind alle möglichen Zustände in der linken Spalte, die möglichen Eingaben in der ersten Zeile. Zustandsübergänge und Ausgaben finden sich dann im inneren der Tabelle. Mehrere mögliche Ein- und Ausgabepaare zu einem Zustand stehen hier in einer Reihe nebeneinander.

Zur Themenübersicht  
Zum Seitenanfang 
Zur vorigen Seite         Zur nächsten Seite  

    © 2001 LK 13 If und G. Kubitz  Hannah-Arendt-Gymnasium, Lengerich