Zur Themenübersicht     

Zur Erinnerung: 

formale Definition einer Sprache E sei ein Eingabealphabet, d.h. eine endliche Menge von Eingabeelementen E = {e1, e2, e 3,…, e n} n Є N Ein Wort ist eine endliche Folge von Elementen aus dem Eingabealphabet. Die Hülle E* von E ist die Menge aller Worte über E und das leere Wort ε.  Eine Sprache ist eine irgendwie definierte Teilmenge L aus E* (L = Language).

Das Erzeugen von Worten einer Sprache mittels einer Grammatik

Eine Grammatik besteht im Wesentlichen aus Regeln. Wir stellen uns einmal eine Grammatik vor, die nur eine Regel besitzt: 
"Ein Satz besteht aus einem Subjekt und einem Pädikat" . In der Formalen Sprache der Informatik wird daraus:

SATZ --> SUBJEKT  PRÄDIKAT    oder noch kürzer:

(R1)    S --> SU  PR    

In einem Schulbuch des ersten Schuljahres mögen am Anfang nur die Subjekte Rolf und Renate und die Prädikate spielt und tanzt vorkommen. In der formalen Sprache der Informatik wird daraus:

(R2)    SU --> Rolf 
(R3)    SU --> Renate
(R4)    PR --> spielt
(R5)    PR --> tanzt

Es handelt sich bei den Regeln R1 bis R5 um ein Regelwerk, das besagt, wodurch die allgemeinen Ausdrücke S, SU und PR jeweils ersetzt werden dürfen. Das Zeichen "-->" lesen wir als: Kann ersetzt werden durch.

Nun können wir mit Hilfe der Regeln R1 bis R5 alle möglichen Sätze bilden: 
Beginnend mit dem Startsymbol S (für Satz) können wir mit Hilfe von Regel1 S ersetzen durch SU  PR und erhalten:

Ersetzen wir nun SU durch Rolf (Regel2) und PR durch spielt (Regel4) , dann erhalten wir: 

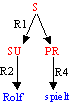
Ersetzen wir aber SU durch Renate (Regel3) und PR durch tanzt (Regel5) , dann erhalten wir: 

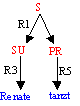
Zwei Sätze, die Rolf und Renate gefallen mögen. Ersetzen wir aber SU und PR ein wenig anders, dann muss Rolf tanzen und Renate hat endlich Zeit zum Spielen:

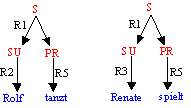
Bevor wir das obige Beispiel verallgemeinern, einige Anmerkungen zu den Begriffen Wort und Satz.:

Die  Elemente des Eingabealphabetes sind Rolf, Renate, tanzt und spielt. Also E = {Rolf, Renate, tanzt, spielt}. 
Die Elemente des Eingangsalphabetes bezeichnen wir umgangssprachlich (leider) als Worte.
Die im formalen Sinne als Worte bezeichneten Kombinationen aus Elementen des Eingabealphabetes sind die oben gebildeten Sätze 'Rolf spielt', Renate tanzt' usw. 

 

Gegenüberstellung der Bezeichnungen:

Bezeichnungen nach der formalen Definition einer Sprache	In unserem Beispiel
Eingabealphabet E	E = { Rolf, Renate, tanzt, spielt }
Wort (= endliche Folge von Elementen aus E)	Satz wie 'Rolf tanzt'

Nun können wir zur formalen Definition kommen:

 

Formale Definition einer Grammatik : Eine Grammatik "G" besitzt eine endlichen Menge  E von Elementen, die nicht mehr ersetzt werden müssen. Sie heißen Terminalsymbole, weil bei ihnen der Ersetzungsvorgang terminiert (endet) .  (Im obigen Beispiel sind dies die blauen Worte) Ferner besitzt eine Grammatik eine endliche Menge N von Symbolen, die ersetzt werden müssen. Sie heißen Nichtterminalsymbole.  (Im obigen Beispiel die roten Symbole) Hinzu kommt ein Regelwerk R, welches festlegt, wie aus diesen Terminalsymbolen durch schrittweise Ersetzung Worte dieser Sprache gebildet werden können.  (Im obigen Beispiel sind dies die Sätze wie Rolf tanzt)  Zusätzlich benötigen wir ein Startsymbol S Î N, mit dem das Bilden von Sätzen stets beginnen muss..

Vereinbarung: 

Terminalsymbole werden meist mit kleinen, Nichtterminalsymbole mit großen Buchstaben geschrieben.

Zur Themenübersicht
Zum Seitenanfang
Zur vorigen Seite	Zur nächsten Seite