Zur Themenübersicht     

Wir beschäftigen uns zur Einführung mit einer einfachen Sprache über E={a,b,c}:

 L = {abⁿc½ n ³ 1}; Bsp: abc, abbbc, abbbbbbbc

Die Sprache besteht also aus allen Worten, die 

1. mit a beginnen, 
2. gefolgt von mindestens einem 
3. bis zu beliebig vielen b's , 
4. an die sich zum Abschluss ein c anschließt.

Es ist sehr einfach, eine zugehörige Grammatik dazu zu definieren:

Die Terminale sind T={a,b,c}, die Nichtterminale N={S, A, B}. 
Das Regelwerk lautet wie folgt (Die Nummerierung entspricht der obigen Nummerierung des Textes):

1. S  --> aA  
2. A --> bB
3. B  --> bB
4. B --> c 

Es ist ebenso einfach einen endlichen Automaten zu konstruieren, der genau diese Sprache akzeptiert.
Das Eingabealphabet ist E={a,b,c}, die Zustandsmenge ist Z={S, A, B}. 

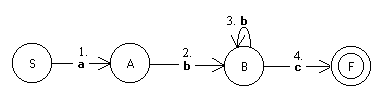
Vergleichen wir die Grammatik mit dem Automaten, dann wird sofort einsichtig, dass nicht nur in diesem Fall sondern immer zu jeder rechtslinearen Grammatik ein endlicher erkennender Automat existiert, der genau die Worte der entsprechenden Sprache erkennt.

Der Automat ist dabei folgendermaßen zu konstruieren:

• Die Eingabemenge E ist gleich der Menge der Terminale T   : E = T
• Die Zustandsmenge ist gleich der Menge der Nichtterminale : Z = N
• Regeln werden auf Automaten folgendermaßen abgebildet:
  

Normalfall 1

Regel	zugehöriger Automat
A --> bB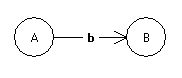

Sonderfall (Hier: Es können beliebig viele Terminale b  eingefügt werden):

Regel	zugehöriger Automat
B --> bB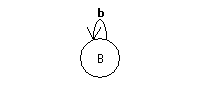

Normalfall2: Nichtterminal kann durch Terminal ersetzt werden:

Regel	zugehöriger Automat
A --> b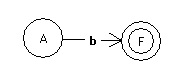

Sonderfall: Nichtterminal kann durch leeres Wort ersetzt werden:

Regel	zugehöriger Automat
A --> e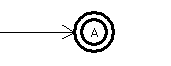

Wir fassen zusammen:

 

Ohne Beweis ist damit folgender Satz zumindest einsichtig:

Rechtslineare Sprachen = von EEA's erkannte Sprachen Zu jeder rechtslinearen Grammatik G gibt es einen endlichen erkennenden Automaten A, der genau die Worte akzeptiert, die von G erzeugt werden. Umgekehrt gibt es zu jedem endlichen erkennenden Automaten A eine rechtslineare Sprache L, so dass der Automat genau die Worte von L erkennt. Oder zusammenfassend: Die Menge der rechtslinearen Sprachen ist genau die Menge der Sprachen, die von endlichen erkennenden Automaten akzeptiert werden. Anmerkung: Der Satz gilt natürlich auch für linkslineare Sprachen

Zur Themenübersicht
Zum Seitenanfang
Zur vorigen Seite	Zur nächsten Seite