Zur Themenübersicht
Unsere bisherigen Überlegungen zum Erkennen von kontextfreien Sprachen durch Kellerautomaten hat ein wesentliches, aber ungelöstes Problem: Woher wei? der Automat, welche Regel er anwenden soll, wenn es für ein Nichtterminalsymbol mehrere Regeln gibt ?
Die Antwort ist nicht trivial.
Eine Möglichkeit besteht darin, Grammatiken so zu formulieren, dass es möglich ist, aus dem aktuellen Eingabezeichen und einer festen Zahl von Folgezeichen der Eingabe eindeutig auf die anzuwendende Regel zu schließen.
Eine Grammatik, die dies ermöglicht heißt 'vorausschauende Grammatik'.
Definition: Eine Grammatik heißt vorausschauend, wenn es eine feste natürliche Zahl k gibt mit folgender Eigenschaft: Aus dem aktuellen Eingabezeichen und den k folgenden Eingabezeichen ist die von einem Kellerautomaten anzuwendende Ersetzungsregel für Nichtterminalsymbole eindeutig festgelegt.
Statt der bekannten nicht vorausschauenden Grammatik :
Grammatik 1:
S ::= ( ) Regel1
S ::= ( S ) Regel2
S ::= S S Regel3
lassen sich wohldefinierte Klammerpaare auch durch folgende Grammatik herleiten:
Grammatik 2:
S ::= ( S ) S Regel1
S ::= e
Regel2 (e bedeutet hier :
Ersetzen durch NICHTS)
Diese Grammatik ist vorausschauend mit k=0, d.h. es genügt schon das aktuelle Eingabezeichen, um die anzuwendende Regel festzulegen.
Um dies einzusehen leiten wir wieder einmal das Klammerpaar ( ( ) ( ) ) her:
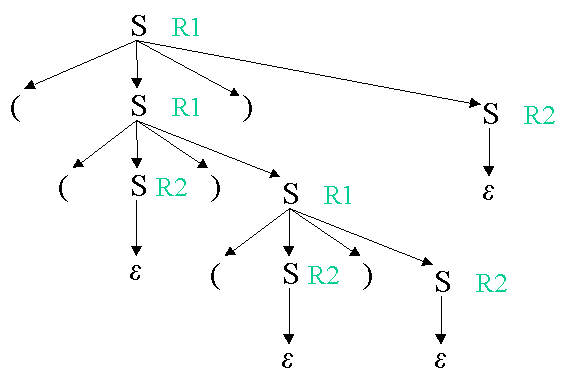
(e bedeutet, dass das Nichtterminal S durch gar nichts ersetzt wird.)
Wir merken uns die Reihenfolge der Ersetzungen (von links nach rechts):
R1, R1, R2, R1, R2, R2, R2
und führen Sie mit Hilfe eines Kellerautomaten durch:
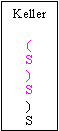
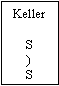
| Anfangszustand: Auf dem Eingabeband liegt die Zeichenfolge ( ( ) ( ) ). Das aktuelle Zeichen ist jeweils rot markiert. Auf dem Keller liegt das Startsymbol der Grammatik: |
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
|
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
( |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
( |
|
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
( |
 |
|
|||
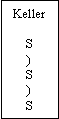| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
( |
 |
|
|||
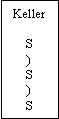| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
S |
|
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
) |
 |
|
|||
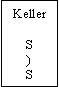| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
( |
|
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
( |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
( |
KZ
( |
|
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
S |
|
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
S |
|
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
) |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
) |
|
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
S |
|
|
|||
| Eingabeband ( ( ) ( ) ) |
EZ
) |
KZ
) |
 |
|
|||
| Eingabeband ( ( ) ( ) ) _ |
EZ ) |
KZ
) |
|
|
|||
| Eingabeband ( ( ) ( ) ) _ |
EZ
|
KZ
S |
 |
|
|||
| Eingabeband ( ( ) ( ) ) _ |
EZ
|
KZ
S |
 |
Auch für diese Grammatik gilt :Wenn Sie sich bis hier hin durchgearbeitet haben, dann dürfen Sie auch dies erfreuliche Ergebnis genießen ;-) :
Das Eingabeband ist leer,
Der Keller ist leer
à Die Eingabezeichenfolge wurde akzeptiert
Ein genauer Blick auf die oben aufgezeic<hnete Arbeit des Kellerautomaten liefert die Antwort: Wenn beim Ersetzen des Nichtterminals 'S' das Eingsbezeichen eine Klammer auf '(' ist, dann wird ersetzt nach Regel 1 S::=(S)S , sonst nach Regel 2 S::=e (nichts).
UND WARUHUM ??
Von den beiden zur Verfügung stehenden Regeln ist Regel 1 halt die einzige, die mit einer Klammer auf beginnt.
Verallgemeinerung:
Wenn es in einer kfS für das gleiche Nichtterminal mehrere Regeln gibt, dann
kann zwischen diesen Regeln vorausschauend unterschieden werden, wenn es eine
feste natürliche Zahl k gibt mit folgender Eingenschaft: Ersetzt man bei diesen
Regeln von links Nichtterminale durch Regeln und/oder Terminale, dann ergeben
sich Folgen von Terminalen, die sich mit Sicherheit nach den ersten k Zeichen
unterscheiden.
| Zur
Themenübersicht |
|
 Zum Seitenanfang |
|
 Zur vorigen Seite |
Zur
nächsten Seite
 |
| © 2001 LK 13 If und G. Kubitz | Hannah-Arendt-Gymnasium, Lengerich |